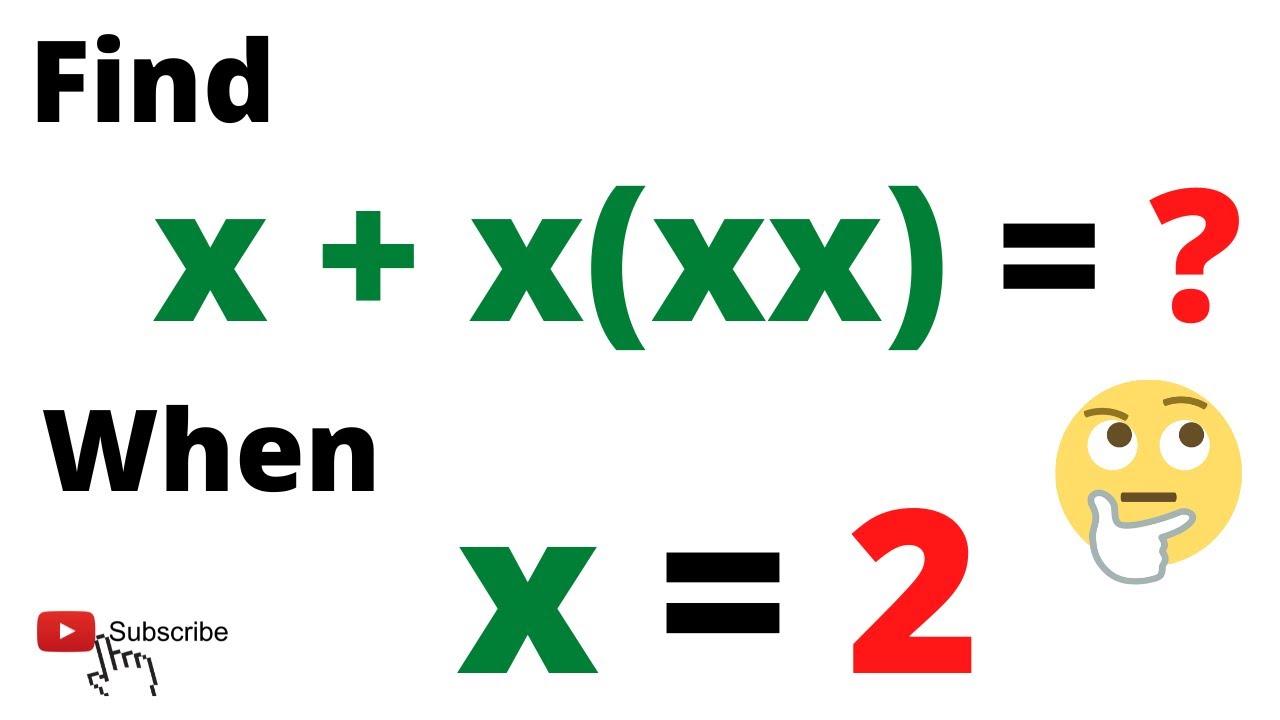Exploring Math: X*x*x, Equations & More!

Are you fascinated by the elegance of mathematical expressions and their practical applications? The seemingly simple act of multiplying a number by itself three times, as in x xx, unveils a profound concept with wide-ranging implications, and can be written as x³. From the fundamental principles of algebra to complex scientific calculations, understanding this operation is crucial for unlocking a deeper comprehension of the world around us.

The expression x³, or "x raised to the power of 3," represents a fundamental operation: cubing a number. It signifies multiplying a number, denoted by 'x', by itself three times. This process is not merely an abstract concept; it's a cornerstone of mathematical modeling, used extensively across diverse fields. Whether in financial forecasting, engineering design, or the exploration of physical phenomena, the ability to manipulate and understand cubic relationships is indispensable. Consider its presence in the calculation of volumes, the modeling of population growth, or the analysis of economic trends. The power of cubing lies in its ability to capture non-linear relationships, adding depth and complexity to our understanding.

Let's delve deeper into the mechanics. When we encounter x³ in mathematical notation, we are instructed to perform x x x. For instance, if x equals 2, then x³ is calculated as 2 2 2, resulting in 8. Similarly, if x equals 3, then x³ equates to 3 3 3, or 27. This operation is not limited to integers; it applies to all real numbers, enabling the exploration of a continuum of values and relationships. Moreover, the power of this expression extends to more abstract applications in solving equations, formulating algorithms, and visualizing data.

• Le Voilier Poem Fact Vs Fiction Blakes Influence Unveiled
• Filmyfly On Tiktok Latest News Updates Discover Now

Consider the case when x³ appears within a more complex equation. Take for instance, a quadratic equation, which, in its standard form, looks like this: ax² + bx + c = 0, where 'x' represents an unknown value and a, b, and c are known constants. The presence of the squared term (x²) suggests the application of the concepts and skills discussed here are also important.

Let's consider the intriguing number 2025 and its mathematical properties. Interestingly, 2025 can be expressed as the sum of cubes of the first nine natural numbers: 0³ + 1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ = 2025. This unique property illustrates the interconnectedness of mathematical principles and the elegance that can be found within numerical relationships. Moreover, 2025 holds additional intrigue; it can be expressed as the product of two perfect squares: 9² * 5², where 9 and 5 are the bases of the squared numbers. This highlights how composite numbers can be decomposed into their fundamental components, demonstrating the underlying principles of number theory. Furthermore, 2025 can also be presented as the sum of three perfect squares, showing the many ways in which numbers can be structured, illustrating the flexibility and versatility of mathematical expressions.

The evolution of computational tools has significantly impacted the way we interact with mathematical concepts. Online calculators, for example, have revolutionized the way we solve equations and explore mathematical relationships. A "solve for x calculator" is an invaluable tool for anyone navigating the intricacies of algebra, simplifying complex equations, and providing a clear understanding of solutions. These tools accept an equation as input and return a solution, often accompanied by steps, clarifying the process and enhancing the learning experience. They can handle equations in one or multiple variables, offering a versatile approach to solving various problems.

• Lana Rhoades Career Facts More Everything You Need To Know
• Kannada Movies 2024 2025 Whats Trending Where To Watch

The use of Roman numerals, although less common in everyday calculations, is another fascinating area of mathematical exploration. Converting Roman numerals to modern numerals is an exercise in deciphering a numerical system that dates back centuries. An online Roman numeral converter is one useful tool that assists individuals in translating between these different systems. The calculator takes a Roman numeral as input and converts it to its modern numeric equivalent. This is a great tool to grasp the historical and cultural context of numerals.

Moving beyond specific calculations and exploring the use of variables is also important. Consider an example with three indeterminates: x + 2xyz - yz + 1. This expression introduces several variables (x, y, and z), illustrating the power of algebra in representing relationships between multiple, unknown quantities. This algebraic notation forms the cornerstone of mathematical modeling and the solution of real-world problems.

Turning to another distinct domain, the world of cinema, we find the XXX film series. While it might initially seem unrelated to the mathematical discussions, the series offers another lens through which to explore the power of numbers. The series, which has achieved commercial success, is a testament to the combined power of storytelling and visual spectacle. The films have grossed hundreds of millions of dollars.

The power of algebraic expressions like x³ and its applications are evident. Moreover, the use of online graphing calculators is a powerful tool for visualizing the patterns in mathematics, allowing users to graph functions, plot points, and animate graphs. This visual approach makes these abstract mathematical concepts more accessible and easily understood.

In the context of financial and professional development, consider the importance of avoiding critical mistakes when preparing documentation, such as descriptive papers for bank applications. Avoiding these issues can be achieved by having a clear understanding of the content, the format, and ensuring accurate grammar.

As we've explored, the expression x³ is a cornerstone of mathematical understanding. It's a tool for calculations, problem-solving, and modeling real-world phenomena. The applications extend into various fields, enhancing our ability to describe, understand, and influence the world around us.

In mathematics, understanding the expression x³ involves grasping the cube of x: x multiplied by itself three times. It is not just an isolated operation but is at the core of algebraic manipulation, geometric calculations, and the modeling of a wide array of phenomena. The ability to work with cubic expressions, along with quadratic and other polynomials, is fundamental for solving problems and gaining insights across scientific and technical disciplines.

The implications of x³ are also applicable in the context of business, education, and research, providing tools to better understand and anticipate financial trends, population dynamics, and other complex systems. The continued exploration of this single expression highlights the lasting significance of the foundational principles of mathematics in a rapidly changing world.